Footnotes

^[1] I have in mind his speech on "Kant's Critique and Cosmology" at the 150th. anniversary of Kant's death (Popper 1965, pp. 175 ff., now also contained in the introduction to the German translation).

^[2] Dr. Elie Zahar has kindly pointed out to me that my description does not take into account the Riemann-Christoffel curvature of space which has nothing to do with the choice of the coordinates. I admit that I am making use of a simplification which is, however, necessary because otherwise my arguments, too, would become unintelligible. The following text will show that, as long as the concept of curved space-in whatever version-is based not on empirical assumptions, but on mathematical inference, my arguments against it remain the same.

^[3] The same argument will apply to any amendment of this theory as, for example, by the Riemann-Christoffel curvature of space, as long as it is purely mathematical and does not introduce new empirical (falsifiable) information.

^[4] I am happy to be able to correct this statement now because it is no longer true: after writing first drafts of this article, but before reading it at the conference, I received a very kind reply from Dr. Thomas Angelidis, London, who spared a tremendous amount of time to go into the details of my criticism and caused me to correct some serious mistakes in earlier versions of this article. Before the conference time was too short to reach a result in our discussion, but some of the footnotes refer to it. And Dr. Elie Zahar, to whom the paper was sent by a common friend, also made some important-critical-comments. As far as possible I discuss these too in the footnotes (see already footnotes 2, 3).

^[5] This argument remains valid even after taking into account the Riemann-Christoffel curvature of space (cp. footnotes 2, 3) as long as this relies on purely mathematical inferences, i.e. without introducing new empirical hypotheses.

^[6] The same appears to have happened with his explanation of the rotation of the long axis of the Mercury-orbit. In (Einstein 1915) he reports that this implied the assumption of a curving of light in the gravitational field twice as strong as previously calculated by him. This was before Eddington's experiment!

^[7] Also in (Einstein 1990, p. 91)

^[8] I doubt the correctness of this interpretation, but this does not affect the validity of the argument against the general theory of relativity since, at any rate, the Hubble effect must be explained somehow.

^[9] Strictly speaking the experiment discussed here must be considered in terms of the general theory of relativity because it deals with circular movements. But since the authors Hafele & Keating (see footnote 10) apply the special theory "as a first approximation" I am doing the same in this article. The distinction between special and general relativity has no bearing on the arguments used in the following text as long as it is agreed that general relativity will also produce a time difference for the clock experiment. Einstein explicitly said so (Einstein 1917, p. 53).

^[10] At this point I have been accused of misunderstanding the special theory of relativity. Both Dr. Angelidis and Dr. Elie Zahar argued that the speed should be taken "with respect to the same inertial frame" (Zahar's words), and that the east-west asymmetry would then be explained by "the different relative speeds involved" (Dr. Angelidis' words). Their argument, I understand, is that the speed of the planes should not be taken relative to USNO where it would be equal, but relative to the axis of the earth, where it must be added to, or subtracted from,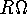

(the rotation velocity of the equator). I think they did not get my point, and I will therefore try to clarify my view with the following two arguments:

According to Hafele & Keating "special relativity predicts that a moving standard clock will record less time compared with (real or hypothetical) coordinate clocks distributed at rest in an inertial reference space" (their words). Let us now assume three satellites, 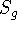, , 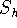, 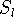each with a clock on board. 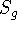is in a geostationary position, rotating with the equator and keeping its place relative to USNO and any other location on earth. 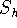is in a "heliostationary" position, keeping its position between the sun and the earth (and therefore not rotating with the equator). And 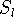is in a "lunarstationary" position, keeping its position between the earth and the moon, and relative to any location on the moon, and therefore rotating around the earth, but not with the equator. Why do Hafele & Keating measure the time difference (only) relative to 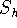? 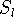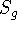Taking would have produced something quite different, and taking would have produced equal relative velocities for both trips. Is there any reason to consider only 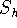to be "at rest", and the others not to be at rest? Since no observer was out in space, or on the North Pole, they could just as well have chosen 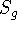or 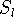as their reference clock. Unless, for some reason, they "prefer" 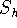. But "preferring" is not permitted by relativity.
Another way of demonstrating the incoherence of the Hafele & Keating experiment and the results obtained by relativity can be found in the following Gedankenexperiment: let a satellite, having on board a caesium beam clock sending time signals to earth, fly on a course shaping a very long ellipse, comparable to the course of Halley's comet relative to the sun, and circumnavigate the earth as its focal point from east to west, i.e. against the direction of its rotation. According to special relativity the time dilatation on this satellite should be strongest (the ageing of the clock should be at its minimum) when its velocity is highest. This would be the point when its course is closest to the earth as its focal point. But the observation made by Hafele & Keating shows that, at this point, when circumnavigating the earth in an east-west direction, the clock on the satellite will in fact be gaining time (ageing faster).

^[11] Popper's words, (Popper 1966, volume 2, p. 9).

^[12] I am referring to chapters 3 & 11 of "The Open Society and its Enemies", (Popper 1966).

^[13] This is a necessary implication of any theory involving the Lorentz transformation. For the expression:

displaymath612

will yield 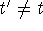for any 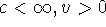. The arguments related to special relativity will therefore remain valid for general relativity as long as general relativity relies on a transfer of the results obtained from an application of the Lorentz transformation in special relativity. This transfer Einstein undertook explicitly in (Einstein 1917, p. 53), when he assumed a time dilatation for a clock mounted on the periphery of a rotating disc.

^[14] At this point I should mention that the hypothesis of the constant spreading velocity of light is also incompatible with the common interpretation of the Hubble effect as an expression of the Doppler principle. Hubble's interpretation relies on the assumption that the redshift of light from distant galaxies is caused by their (assumed) flight movement which will, according to the Doppler principle, reduce frequency, as we can all observe when we hear the horn of a passing car. But this presupposes that the velocity of the (assumed) flight movement can be deducted from the velocity of light coming from distant galaxies. The Doppler principle will never yield a difference of frequency without difference of velocity. But this clashes with Einstein's principle of the constant spreading velocity of light which explicitly excludes an addition, or subtraction, to or from the velocity of light. Therefore the common interpretation of the Hubble effect as an expression of the Doppler principle is also incompatible with the theory of relativity.

^[15] This is a somewhat rash conclusion which, for time reasons, it was impossible to elaborate when actually reading the paper at the conference, and of which only a sketchy outline can be given here. It is clear that, even if the time difference observed by Hafele & Keating cannot be explained by special relativity, as I have tried to show in the text (par. 22), the refutation of special relativity will not explain it either. We need a new empirical hypothesis, and time dilatation can be explained if we assume the earth and its surrounding atmosphere to be a vortex-like rotating field of energy (ether) in which matter is a form of appearance (comparable to a disturbance) of that field. The clock flying eastward is then flying with the direction of rotation, the other one against it, and all the time the field is "flowing" through both clocks, and their time difference is accounted for by the Doppler principle which would otherwise be incompatible with the assumption of a constant spreading velocity of light (see footnote 14). The "time difference" is then, in fact, a difference of performance: one of the clocks has gone through more oscillations of the field than the other.

^[16] The formula in footnote 13 is needed only to make the contradiction clearer for adherents of relativity; my criticism of the theory of relativity could do without it.

^[17] Here again I am referring to chapters 3 & 11 of The Open Society and its Enemies, (Popper 1966).

^[18] There are many examples in his texts. In (Einstein 1917, p. 13) he says: "This is where the theory of relativity sets in. By an analysis of the physical concepts of "time" and "space" [he did not put quotation marks] it appeared that, in reality, there is no incompatibility of the relativity principle with the law of spreading velocity of light, but that systematic application of both these laws will yield a logically faultless theory"-(his italics; my translation). I think this shows quite clearly that he thought he was working exclusively by logical inference.

tcr-editors@www.eeng.dcu.ie